Inverse Demand, WTP and CS
Inverse Demand
Inverse Demand
Inverse demand is a function which shows for a set of possible quantities, the prices at which each of those quantities is demanded.
That is, while demand is a function from
$$
\text{ price } \rightarrow \text{ quantity demanded}
$$
inverse demand is a function from
$$
\text{ quantity demanded } \rightarrow \text{ price }
$$
Example 1: Inverse Demand
The figure below shows Jenna's inverse demand for coffee.
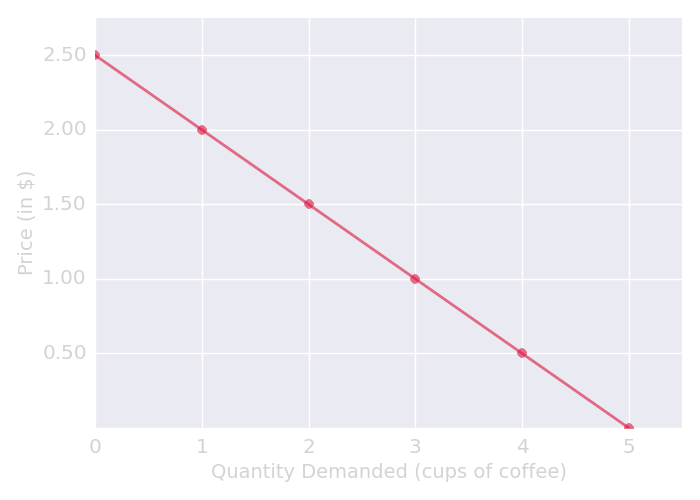
Example 2: Inverse Demand
Jenna's demand for coffee is given by:
\begin{equation}
Q_{d} = 5 - 2P
\end{equation}
What is her inverse demand for coffee?
\begin{equation} P = \frac{5 - Q_{d}}{2}. \end{equation}
Willingness-to-pay (WTP)
Willingness-to-pay (WTP)
Definition (Individual WTP): An individual's willingness-to-pay (WTP) for any given unit of a product or service, is the maximum amount that the individual is willing (and able) to pay for the unit.
Definition (WTP in the market): Willingness-to-pay (WTP) for any given unit of a product or service in the market is the maximum amount that some individual in the market is willing (and able) to pay for that unit.
Finding WTP given Demand
- Graphically, given a demand curve, WTP for any unit is the vertical distance to the demand curve. (Why?)
- Given a demand equation, WTP for \( k^{\text{th}} \) unit is the price at which quantity demanded is \( k \). That is, use the inverse demand to find price at which quantity demanded is \( k \).
Example 1: Willingness-to-pay (WTP)
Example 2: Jill's WTP for coffee
Suppose Jill's monthly demand for coffee is given by:
\begin{equation}
Q_{d} = 100 - 20P,
\end{equation}
(a) What is her willingness-to-pay (WTP) for the 10th cup of coffee in a month?
(b) What is her willingness to pay for 20th cup of coffee?
See below for solution of part (a).
Solution of part (a)
Using Jill's demand function we obtain her inverse demand:
\begin{equation}
P = \frac{100 - Q_{d}}{20}.
\end{equation}
Now substitute \( Q = 10 \) in the inverse demand. Doing so, gives: \begin{equation} P = 4.50. \end{equation}
Consumer Surplus
Consumer Surplus (CS)
Consumer surplus on any unit of a product is the difference in WTP for that unit and the price of that unit:
CS of a unit = (WTP for that unit) - (Price of the unit)
Adding consumer surplus across all units consumed by a consumer gives the total consumer surplus enjoyed by the consumer.
Adding consumer surplus across all units consumed in a market gives the total consumer surplus in the market.
Calculation of Consumer surplus (CS)
When calculating total CS across given units we can use two methods:
Method 1: Calculate consumer surplus for each unit (using the definition on previous slide) and add the CS across different units.
Method 2: Calculate CS as the area below the demand curve and above the price for the given range of units.
Example of Method 1
Calculate consumer surplus when price = $15.
\begin{align} CS &= (30 - 15) + (25 - 15) + (20 - 15) + (15 - 15) \nonumber\\ &= $30. \nonumber \end{align}
Example of Method 2
Calculate consumer surplus when price = $15.
$$ CS = \frac{1}{2} \times (35-15) \times 4 = $40. $$
Should I use Method 1 or Method 2?
Depends on the data and the problem. If you have discrete data, such as in a table then you have to use Method 1.
If you have continuous data, such as a graph of a demand curve, or functional form of demand, then use Method 2.
Even when you have continuous data, if you want to calculate CS for some specific, non-consecutive units then use Method 1.
In short, use method 1 when method 2 cannot really be used; otherwise, use Method 2.
Practice Problem: WTP and CS
Consider the following market demand: $$ Q_{d} = 100 - 5p $$
- Calculate WTP for each of the following units: 20, 50, 75.
- Calculate the CS for each of the units listed in part 1, assuming that price is $4.
- Calculate the total CS in the market when market price is $4. (Hint: As noted on a previous slide, you can calculate CS as an area enclosed by the demand curve, horizontal line at market price and the vertical axis.)
Loss of consumer surplus in market for Jeans
The following example from Acemoglu et al.'s text shows how the notion of consumer surplus can be used to evaluate losses in the market for jeans.
One of the authors of the book was working on policies to reduce groundwater contamination. One option was to prohibit use of certain chemical treatments on fabrics. Assume that doing so would increase the price of jeans from $50 to $75.
Clearly, the price increase is a loss for consumers. But how do we quantify this loss, so that we can compare it with any gains. This is where consumer surplus comes to help.
Loss of consumer surplus in market for Jeans